Question

Mr. Frey hits the squirrel (don't worry, it survived with just minor injuries) and he went flying through the air leaving his bike behind. He hits the ground and skids to a

stop accelerating at 4.92m/s2 slowing down(don't worry, he survived with major injuries). What is mew between Mr. Frey and the cement?

Mr Frey is 90kg

His bike is 200kg

Use 9.8 for acceleration of gravity

Answer 1

μ ≈ 0.458

Step-by-step explanation:

To solve the problem involving Mr. Frey's accident, we must determine the coefficient of friction ( denoted as μ) between Mr. Frey and the cement as he skids to a stop. The coefficient of friction is a dimensionless scalar value that represents the frictional resistance between two surfaces in contact.

Given that Mr. Frey is slowing down with an acceleration of 4.92m/s², we know that this is the acceleration caused by the frictional force exerted by the cement on Mr. Frey. The frictional force (f) can be calculated using Newton's second law of motion, F = ma, where 'm' is the mass of the object (Mr. Frey in this case), and 'a' is the acceleration.

The only force acting horizontally is friction, which is equal to the product of the normal force (n )and the coefficient of friction 'μ'. The normal force in this situation is equivalent to the weight of Mr. Frey, which is 'mg', with 'g' being the acceleration due to gravity. We have:

`\Longrightarrow \vec f_k = m \vec a \\\\ \\\\\Longrightarrow \mu _k \vec n = m \vec a \\\\\\\\\Longrightarrow \mu _k mg = m \vec a\\\\\\\\\Longrightarrow \mu _k =(m \vec a)/( mg) \\\\\\\\\therefore \mu _k =( \vec a)/( g)`

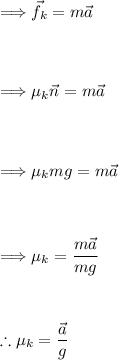
Plugging in our values, we get:

`\Longrightarrow \mu _k =( 4.49 \ m/s^2)/(9.8 \ m/s^2)\\\\\\\\\therefore \boxed{\mu_k \approx0.458}`

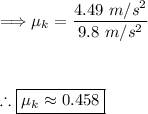
Thus, μ ≈ 0.458.