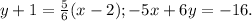Question

7. A line passes through (2, -1) and (8, 4). Writean equation for the line in point-slope form.Rewrite the equation in standard form using integers.y + 1 = %(x+ 2); -5x + 6y = -16•y-1=2(0x-2); -5x+ 6y= 16y-2=%0x+1);-5x+ 6y=17•y+1= %k-2);-5x+ 6y= -16

Answer 1

Recall that the equation of a line that passes through two points is given by the following formula:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1).`

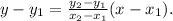
Notice that the above formula gives us the equation of the line in point-slope form. Substituting the given values in the above formula, we get:

`y-(-1)=(-1-4)/(2-8)(x-2).`

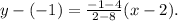
Simplifying the above result, we get:

`y+1=(5)/(6)(x-2).`

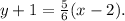
Now, taking the above equation to its standard form, we get:

`\begin{gathered} 6y+6=5(x-2), \\ 6y+6=5x-10, \\ 6y-5x=-10-6, \\ -5x+6y=-16. \end{gathered}`

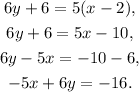
Answer:

`y+1=(5)/(6)(x-2);-5x+6y=-16.`