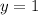For a conic with a focus at the origin, if the directrix is
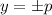
where p is a positive real number, and the eccentricity is a positive real number e, the conic has a polar equation
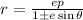
if 0 ≤ e < 1 , the conic is an ellipse.
if e = 1 , the conic is a parabola.
if e > 1 , the conic is an hyperbola.
In our problem, our equation is
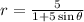
If we compare our equation with the form presented, we have
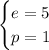
Therefore, the directrix is