Given the next quadratic equation:
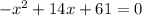
we can use the quadratic formula to solve it, as follows:
![\begin{gathered} x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ x_(1,2)=\frac{-14\pm\sqrt[]{14^2-4\cdot(-1)\cdot61}}{2\cdot(-1)} \\ x_(1,2)=\frac{-14\pm\sqrt[]{196+244}}{-2} \\ x_(1,2)=\frac{-14\pm\sqrt[]{440}}{-2} \\ x_1=\frac{-14+\sqrt[]{440}}{-2}=(-14)/(-2)-\frac{\sqrt[]{440}}{2}=7-\sqrt[]{110} \\ x_2=\frac{-14-\sqrt[]{440}}{-2}=(-14)/(-2)+\frac{\sqrt[]{440}}{2}=7+\sqrt[]{110} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/xilwstzzsfu9t1v4udh7.png)
The rounded values (two decimal places) are:
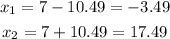
Since x is the distance, in ft, from the sprinkler, it cannot be negative, then the answer which makes sense in the context of this problem is 17.49 ft