Question

The admission fee at an amusement park is $1.50 for children and $4 for adults. On a certain day, 277 people entered the park, and the admission fees collected totaled 828.00 dollars. How many children and how many adults were admitted?

Answer 1

Given:

Let x be the number of children.

Let y be the number of adults.

In total, there were 277 people.

So,

`x+y=277\ldots\ldots\ldots(1)`

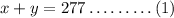
According to the question, the fee of $1.50 for children and $4 for adults and the total fees collected is $828.

So,

`1.5x+4y=828\ldots\ldots\ldots(2)`

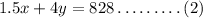
Multiply by 4 in equation (1),

`4x+4y=1108\ldots\ldots\ldots(3)`

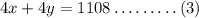
Subtracting the equation (2) from (3), we get

`\begin{gathered} 2.5x=280_{} \\ x=112 \end{gathered}`

Substitute x=112 in equation (1), we get

`\begin{gathered} 112+y=277 \\ y=165 \end{gathered}`

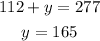
Thus,

• The number of children is x = 112.

,

• The number of adults is y = 165.