Question

Tallulah invested $75,000 in an account paying an interest rate of 7, start fraction, 5, divided by, 8, end fraction7 8 5 ​ % compounded quarterly. magan invested $75,000 in an account paying an interest rate of 7, start fraction, 7, divided by, 8, end fraction7 8 7 ​ % compounded continuously. after 15 years, how much more money would magan have in his account than tallulah, to the nearest dollar?

Answer 1

To find out how much more money Magan would have than Tallulah after 15 years, we can use the formula for compound interest. For Tallulah, the interest rate is 7.875% compounded quarterly, and for Magan, the interest rate is 7.875% compounded continuously. We can calculate the amount for both and find the difference. Magan would have approximately $2,294.85 more than Tallulah in his account after 15 years.

Step-by-step explanation:

To find out how much more money Magan would have than Tallulah after 15 years, we can use the formula for compound interest. For Tallulah, the interest rate is 7.875% compounded quarterly. The formula for compound interest is
`\rm A = P(1+r/n)^{(nt)`, where A is the final amount, P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded per year, and t is the number of years. For Magan, the interest rate is 7.875% compounded continuously. We can calculate the amount for both and find the difference:

Tallulah:
`\rm A = 75000(1+0.07875/4)^((4** 5)) = $190,515.94`

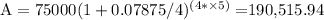
Magan:
`A = 75000e^((0.07875* 15)) = $192,810.79`

The difference between the two amounts is $192,810.79 - $190,515.94 = $2,294.85. Therefore, Magan would have approximately $2,294.85 more than Tallulah in his account after 15 years.

Answer 2

Magan would have approximately $5,454.39 more in his account than Tallulah after 15 years.

Step-by-step explanation:

While both accounts start with the same amount and have similar interest rates, continuous compounding offers a slight edge over quarterly compounding due to more frequent interest accrual. Here's the breakdown:

Tallulah's Account:

Interest rate per quarter = 7.875% / 4 = 1.96875%

Compound interest formula for quarterly compounding = P*(1+r/100)^n

Future value after 15 years with 60 quarters = $75,000 * (1 + 0.0196875)^60 ≈ $205,327.88

Magan's Account:

Continuously compounded interest formula = P*e^(rt)

Future value after 15 years = $75,000 * e^(0.07875*15) ≈ $210,782.27

Difference:

Magan's account will have $210,782.27 - $205,327.88 ≈ $5,454.39 more than Tallulah's account after 15 years.