Question

Two number cubes are rolled what is the probability that the sum of the numbers rolled is either a 1 and a 4 in either order

Answer 1

The first thing we have to know is that a cube with numbers is a dice that has 6 faces and that its numbers go from 1 to 6, so the probability that the sum of both dice gives 1 is zero, since the minimum that we are going to give is 2

`P(sum=1)=0`

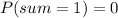
Now for the sum of both dice of 4 we have the following combinations

• 1 and 3

,

• 3 and 1

,

• 2 and 2

We have 3 combinatorics that we have to get the probability of each of the combinations in order to find our final probability

`\begin{gathered} P(1|3)=P(1)P(3)=(1)/(6)\cdot(1)/(6)=(1)/(36) \\ P(3|1)=P(3)P(1)=(1)/(6)\cdot(1)/(6)=(1)/(36) \\ P(2|2)=P(2)P(2)=(1)/(6)\cdot(1)/(6)=(1)/(36) \end{gathered}`

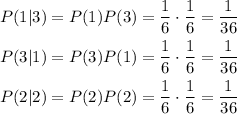
The probability that the sum of 4 would be the sum of the probabilities of the combinatorcs

`\begin{gathered} P(sum=4)=P(1|3)+P(3|1)+P(2|2) \\ P(sum=4)=(1)/(36)+(1)/(36)+(1)/(36) \\ P(sum=4)=(3)/(36) \\ P(sum=4)=(1)/(12) \end{gathered}`

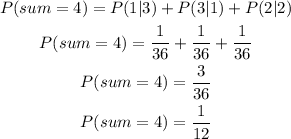
What is the probability of getting a 1 and a 4 in either order?

The probability of getting any number on a die will be 1/6 if we can get a 1 or a 4 then our population will be 2/6

`\begin{gathered} P(1|4)=(2)/(6) \\ P(4|1)=(2)/(6) \\ P(1\&4)=(2)/(6)\cdot(2)/(6) \\ P(1\&4)=(4)/(36) \\ P(1\&4)=(1)/(9) \end{gathered}`