Question

Multiply: - 4x(3x + 2y)(x - 5y).​

Answer 1

Firstly let's multiply within brackets

• -4x[3x(x-5y)+2y(x-5y)]
• -4x(3x^2 -15xy +2xy -10y^2)

Add the like terms

• -4x(3x^2 -13xy -10y^2)

Perform multiplication for the rest of the equation

• -12x^3 +52x^2y + 40xy^2

Thus, our final answer is -12x^3 +52x^2y + 40xy^2 .

Answer 2

`\sf -12x^3 + 52x^2y + 40xy^2`.

Explanation:

To multiply the given expression
`\sf -4x(3x + 2y)(x - 5y)`, we can use the distributive property and the FOIL method (First, Outer, Inner, Last).

Definition:

The distributive property is a mathematical property that states that multiplication distributes over addition and subtraction.

The distributive property can be written in two ways:

a(b + c) = ab + ac

a(b - c) = ab - ac

where a, b, and c are any numbers.

The FOIL method is a mnemonic device for remembering the distributive property when multiplying two binomials. It stands for First, Outer, Inner, and Last.

To use the FOIL method, we multiply the terms in the first parentheses with the terms in the second parentheses, in the following order:

• First terms
• Outer terms
• Inner terms
• Last terms

Let's break it down step by step:

Multiply the terms in the parentheses:

`\sf (3x + 2y)(x - 5y)`

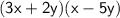
Apply FOIL:

`\sf = 3x \cdot x - 3x \cdot 5y + 2y \cdot x - 2y \cdot 5y`

`\sf = 3x^2 - 15xy + 2xy - 10y^2`

`\sf = 3x^2 - 13xy - 10y^2`

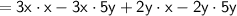
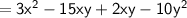
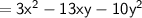
Multiply the result by
`\sf -4x`:

`\sf -4x(3x^2 - 13xy - 10y^2)`

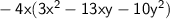
Apply the distributive property:

`\sf = -4x \cdot 3x^2 + (-4x) \cdot (-13xy) + (-4x) \cdot (-10y^2)`

`\sf = -12x^3 + 52x^2y + 40xy^2`

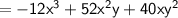
So, the result of the multiplication
`\sf -4x(3x + 2y)(x - 5y)` is
`\sf -12x^3 + 52x^2y + 40xy^2`.