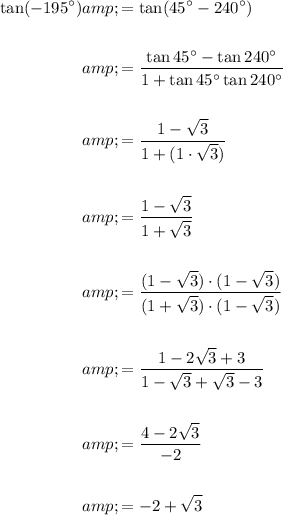Question

Find the exact values of the sine, cosine, and tangent of the angle.

-195° = 45° - 240°
sin(-195⁰) =
cos(-195⁰)=
tan(-195⁰) =

Answer 1

`\sin(-195^(\circ))=\boxed{(√(6)-√(2))/(4)}`

`\cos(-195^(\circ))=\boxed{-(√(6)+√(2))/(4)}`

`\tan(-195^(\circ))=\boxed{-2+√(3)}`

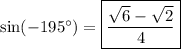
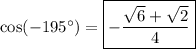
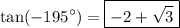
Explanation:

To find the exact values of sine, cosine and tangent of the angle, we can use the angle sum formulas:

`\boxed{\begin{array}{l}\underline{\text{Angle\;Sum\;Formulas}}\\\\\sin (A \pm B)=\sin A \cos B \pm \cos A \sin B\\\\\cos (A \pm B)=\cos A \cos B \mp \sin A \sin B\\\\\tan (A \pm B)=(\tan A \pm \tan B)/(1 \mp \tan A \tan B)\end{array}}`

Rewrite -195° as 45° - 240°.

Therefore, the exact value of sin(-195°) can be calculated as follows:

`\begin{aligned}\sin(-195^(\circ))&= \sin(45^(\circ)-240^(\circ))\\\\&=\sin 45^(\circ) \cos 240^(\circ)-\cos45^(\circ) \sin 240^(\circ)\\\\&=(√(2))/(2)\cdot \left(-(1)/(2)\right)-(√(2))/(2)\cdot \left(-(√(3))/(2)\right)\\\\&=-(√(2))/(4)+(√(6))/(4)\\\\&=(√(6)-√(2))/(4)\end{aligned}`

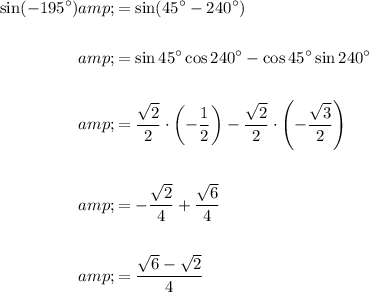
The exact value of cos(-195°) can be calculated as follows:

`\begin{aligned}\cos(-195^(\circ))&= \cos(45^(\circ)-240^(\circ))\\\\&=\cos 45^(\circ) \cos 240^(\circ)+\sin 45^(\circ) \sin 240^(\circ)\\\\&=(√(2))/(2)\cdot \left(-(1)/(2)\right)+(√(2))/(2)\cdot \left(-(√(3))/(2)\right)\\\\&=-(√(2))/(4)-(√(6))/(4)\\\\&=-(√(6)+√(2))/(4)\end{aligned}`

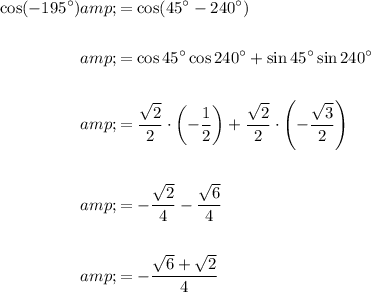
The exact value of tan(-195°) can be calculated as follows:

`\begin{aligned}\tan(-195^(\circ))&= \tan(45^(\circ)-240^(\circ))\\\\&=(\tan 45^(\circ)- \tan 240^(\circ))/(1+\tan 45^(\circ)\tan 240^(\circ))\\\\&=(1-√(3))/(1+(1\cdot √(3)))\\\\&=(1-√(3))/(1+√(3))\\\\&=((1-√(3))\cdot (1-√(3)))/((1+√(3)) \cdot (1-√(3)))\\\\&=(1-2√(3)+3)/(1-√(3)+√(3)-3)\\\\&=(4-2√(3))/(-2)\\\\&=-2+√(3)\end{aligned}`