Question

Jotham needs 12 liters of a 20% alcohol solution. He has a 10% and a 50% solution available. How many liters of the 10% and how many liters of the 50% solutions should he mix to make the 20% solution?

Answer 1

Given:

There are given that the Jotham needs 12 litters of 20% alcohol solution.

Step-by-step explanation:

Let x be the volume of the 50% solution needed

Then,

The volume of the 10% solution to mix is:

`(12-x)`

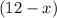
Then,

The equation to find x is:

`0.50x+0.10*(12-x)=0.20*12`

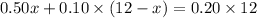
That means,

It say that the volume of the pure alcohol in ingredients is equal to the volume of pure alcohol.

Then,

From the above equation, calculate the value of x

So,

`\begin{gathered} 0.50x+0.10*(12-x)=0.20*12 \\ 0.50x+0.10\cdot12-0.10x=0.20\cdot12 \\ 0.40x+0.10\cdot12=0.20\cdot12 \\ 0.40x=0.20\cdot12-0.10\cdot12 \\ x=(12(0.1))/(0.40) \\ x=3 \end{gathered}`

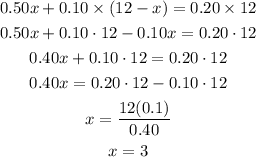
Final answer:

For the 50%, there are 3 litters solution and for the 10%,

`\begin{gathered} 12-x=12-3 \\ =9 \end{gathered}`

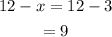
Hence, 3 liters of the 50% solution and 9 liters of the 10% solution.