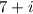Question

Find the remaining zer Degree 3; zeros: 5, 7- i The remaining zero(s) of f is

Answer 1

The remaining zero is;

`7+i`

Step-by-step explanation:

Given that two of the zeros of a polynomial are;

`\begin{gathered} 5 \\ 7-i \end{gathered}`

to get the remaining zero.

Recall that according to complex conjugates, complex roots/zeros comes in pairs;

`\begin{gathered} a+bi \\ \text{and} \\ a-bi \end{gathered}`

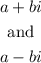
where a and b are real numbers.

Applying the rule to the given roots.

Since we have a complex root;

`7-i`

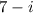
we must also have the other pair of the complex root;

`7+i`

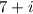
Therefore, the remaining zero is;

`7+i`