Question

I vaguely remember how to do this although I am familiar with all. All I need is a quick review explanation and I’ll be good. Thanks!

Answer 1

We have to calculate the perimeter of a pen that has an area expressed as

A = 3x²-7x+2.

We assume it is a rectangular pen, so it will have two different sides.

The area will be the product of this two side lengths, while the perimeter will be 2 times the sum of the lengths of the two sides.

Then, we start by rearranging the expression of A as a product of two factors.

We can do it by factorizing A.

To do that, we calculate the roots of A as:

`\begin{gathered} x=\frac{-(-7)\pm\sqrt[]{(-7)^2-4\cdot3\cdot2}}{2\cdot3} \\ x=\frac{7\pm\sqrt[]{49-24}}{6} \\ x=\frac{7\pm\sqrt[]{25}}{6} \\ x=(7\pm5)/(6) \\ \Rightarrow x_1=(7-5)/(6)=(2)/(6)=(1)/(3) \\ \Rightarrow x_2=(7+5)/(6)=(12)/(6)=2 \end{gathered}`

Then, we can now express A as:

`\begin{gathered} A=3(x-(1)/(3))(x-2) \\ A=(3x-1)(x-2) \end{gathered}`

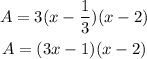
Then, we can consider the pen to be a rectangle (or maybe square, depending on the value of x) with sides "3x-1" and "x-2".

Then, we can now calculate the perimeter as 2 times the sum of this sides:

`\begin{gathered} P=2\lbrack(3x-1)+(x-2)\rbrack \\ P=2(3x-1+x-2) \\ P=2(4x-3) \\ P=8x-6 \end{gathered}`

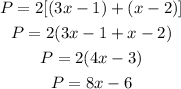
Answer: we can express the perimeter as 8x-6.