Question

I need help answering the “explain how you found the slope and y intercept question. I did not know how to do this and mainly guessed and got the right answer so I need help explaining please

Answer 1

When we are given a straight line drawn on the cartesian graph, i.e, having x and y coordinates, the gradient/slope is the change on the y-axis relative to change on the x-axis.

The x-axis is the horizontal axis and the y-axis is the vertical axis.

To get the gradient, we simply pick two points on the line and name them points 1 and 2. Thus, they will have the following attributes:

`\begin{gathered} Point1=(x_1,y_1) \\ Point2=(x_2,y_2) \end{gathered}`

The gradient of a straight line is:

`s=(y_2-y_1)/(x_2-x_1)`

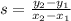
So, in our question, we can pick our points 1 and 2 at

Point 1 = (-2, 6), (1,-3),

Point 2 = (0, 0), (2,-6)

Applying our formulae, we get:

`\begin{gathered} s=\frac{0-6}{0-(-2)_{}}=-(6)/(2)=-3 \\ s=(-6-(-3))/(2-1)=-(3)/(1)=-3 \\ \text{Any two points will give us a gradient of -3} \end{gathered}`

The gradient is -3.

As for the intercept on the y-axis, this is the point on the vertical axis where the graph cuts the graph. It can be visibly seen from our graph as occurring at y = 0.

However, it can be calculated via a formula to give us the form: y = mx + c.

where: m is the gradient/slope and c is the intercept on the y axis.

Formulae for getting conventional line equation is:

`\begin{gathered} (y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1) \\ (y-6)/(x-(-2))=-3 \\ -3x-6=y-6 \\ \text{Adding 6 to both sides gives:} \\ -3x=y \end{gathered}`

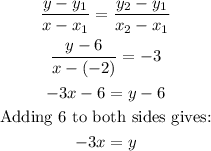
The line equation is therefore: y = -3x + 0

Slope = -3 AND

y-intercept = 0