Question

Water flows with a velocity of 1.50 m/s through a tube with an internal diameter of 1.10 cm. As it exits the tube, the fluid velocity through the nozzle increases to 10 m/s. What is the inside diameter of the nozzle? You can treat the tube as a long cylinder so that the cross-sectional area both in the interior of the tube and the nozzle is the area of a circle.Group of answer choices

Answer 1

2.1 mm

Step-by-step explanation:

I check it the 4.2mm answer is WRONG

Answer 2

In order to calculate the inside diameter, we can use the following relation, since the volumetric flow is constant for any part of the tube:

`\begin{gathered} Q_1=Q_2 \\ A_1V_1=A_2V_2 \end{gathered}`

Where A is the cross-section area and V is the velocity.

Using V1 = 1.5 m/s, A1 = π*1.1²/4 and V2 = 10 m/s, we have:

`\begin{gathered} (\pi\cdot1.1^2)/(4)\cdot1.5=A_2\cdot10 \\ (\pi\cdot1.1^2)/(4)\cdot1.5=(\pi\cdot d^2_2)/(4)\cdot10 \\ 1.1^2\cdot1.5=d^2_2\cdot10 \\ 1.21\cdot1.5=d^2_2\cdot10 \\ 1.81=d^2_2\cdot10 \\ d^2_2=0.181 \\ d_2=0.42\text{ cm}=4.2\text{ mm} \end{gathered}`

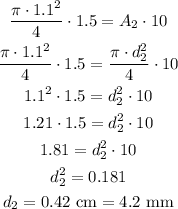
Therefore the correct option is the first one.