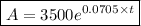Question

Sophie has eamed $3500 working at the movie theater decides to put her money in the bank in an account that has a 7.05% interest rate that is compounded continuously write an equation to model this!

Answer 1

Step 1. The information we have is.

The initial amount of the investment which is called the principal P is:

`P=3500`

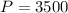
The interest rate is 7.05%, this will be r:

`r=7.05\text{ percent}`

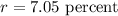
We will need to represent the interest rate as a decimal number, for that, we divide by 100:

`\begin{gathered} r=(7.05)/(100) \\ \downarrow \\ r=0.0705 \end{gathered}`

As additional variables, we will have:

`\begin{gathered} A\longrightarrow\text{Total amount} \\ t\longrightarrow\text{time of the investment} \end{gathered}`

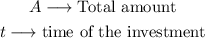
Step 2. Use the Continuous compounding formula:

`A=Pe^(rt)`

where A is the amount including interest, P is the principal amount of the investment, r is the interest rate, and t in years.

Also, e is a constant which is equal to:

`e\approx2.783`

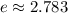
But we will only represent it as e.

Step 3. Substitute P and r into the continuous compounding formula:

`\boxed{A=3500e^(0.0705* t)}`

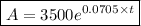
That is the equation that models the situation.

Answer:

`\boxed{A=3500e^(0.0705* t)}`