The exercise describes an exponential decay, you can express this using the general form:
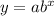
Where
a is the initial amount
b is the decay factor
x is the time intervals
y is the amount after x time intervals
The half-life of a substance indicates the time it takes for the amount to decrease by half.
If the initial amount is a=5 grams, the half-life indicates that after x=20 days, the amount will be
y= 5/2 = 2.5 grams.
You can replace these values on the formula above to obtain an expression where the decay factor will be the only unknown:
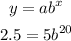
To solve for b, first, divide both sides of the equation by 5:
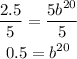
Then apply the square root with index 20 to both sides of the equal sign no reach the value of b:
![\begin{gathered} \sqrt[20]{0.5}=\sqrt[20]{b^(20)} \\ b=0.97 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/khgryv8ytz6fysxh6lcs.png)
Now that you know the value of the decay factor, you can determine how much time it will take for the substance to decrease to 2grams.
The expression for the exponential decay in this case is:
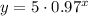
For y=2grams:

Now, you have to solve the expression for x:
-Divide both sides by 5:
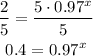
-Apply the logarithm to both sides of the equal sign:
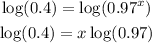
-Divide both sides by the logarithm of 0.97 to determine the value of x:
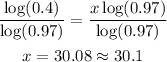
It will take approximately 30.10 days to have 2 grams of substance left.