Question

Classify the systems of equations as consistent dependent, consistent independent,or inconsistent

Answer 1

Recall that:

1) A system of 2 equations is inconsistent if both equations represent different parallel lines.

2) A system of 2 equations is consistent dependent if the equations are equivalent.

3) A system of 2 equations is consistent independent if the slopes of both equations are different.

A) Multiplying the second equation by 2 we get:

`\begin{gathered} (1)/(2)y*2=(x-2)*2, \\ y=2x-4. \end{gathered}`

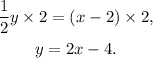
Notice that the above equation is the same as the first equation, therefore the equations of the first system of equations are equivalent, then the system is consistent dependent.

B) Notice that the slope of both equations is 4, also, notice that the y-intercept of the first equation is (0,2), and the y-intercept of the second equation is (0,-3), therefore the equations of the system of equations represent different parallel lines, then the system is inconsistent.

C) Notice that the slope of the first equation is 5 and the slope of the second one is 6, therefore the system of equations is consistent independent.

Answer:

A) Consistent dependent.

B) Inconsistent.

C) Consistent independent.