Question

Given the following reaction:2 Li (s) + 2 H2O (I) = 2 LiOH (aq) + 1 H2 (g)How many grams of solid lithium must be used in this reaction in order to obtain 6.00 L of hydrogen gas at 1.10 atm and 25.0 C ?

Answer 1

3.73 g of Li.

Step-by-step explanation:

What is given?

Volume of hydrogen gas, H2 (V) = 6.00 L.

Pressure (P) = 1.10 atm.

Temperature (T) = 25.0°C + 273 = 298 K.

R = 0.082 L*atm/mol*K.

Step-by-step solution:

First, we have to find the number of moles of hydrogen gas (H2) using the ideal gas formula:

`PV=nRT,`

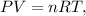
where P is pressure, V is volume, n is the number of moles, R is the ideal gas constant and T is the temperature on Kelvin scale. So let's solve for 'n' and replace the given values:

`n=(PV)/(RT)=\frac{1.10\text{ atm}\cdot6.00\text{ L}}{0.082\text{ }(L\cdot atm)/(mol\cdot K)\cdot298K}=0.270\text{ moles.}`

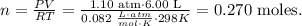
Based on this, we have 0.270 moles of H2.

You can see in the chemical equation that 2 moles of Li reacted produce 1 mol of H2, so we have to state a rule of three:

`\begin{gathered} 2\text{ moles Li}\rightarrow1\text{ mol H}_2 \\ ?\text{ moles Li}\rightarrow0.270\text{ moles H}_2 \end{gathered}`

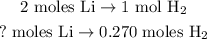
The calculation will look like this:

`0.270\text{ moles H}_2\cdot\frac{2\text{ moles Li}}{1\text{ mol H}_2}=0.540\text{ moles Li.}`

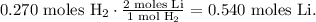
The final step is to convert 0.540 moles of Li to grams using its molar mass that can be found in the periodic table, which is 6.9 g/mol:

`0.540\text{ moles Li}\cdot\frac{6.9\text{ g Li}}{1\text{ mol Li}}=3.73\text{ g Li.}`

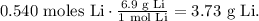
The answer is that we must use 3.73 g of Li to produce 6.00 L of H2 at 1.10 atm and 25.0 °C.