Answer: x = -2 and y = -5
We are given two system of equations
-6x - 2y = 22 ---------------- equation 1
-12x + 10y = - 26------------- equation 2
These two system of equations can be solve simultaneously using elimination method
Before we can apply elimination method, we need to make one of the variables equal in both equations
Let us eliminate x
To make the co -efficient of x equal in both equations, Multiply equation 1 by 2 and equation 2 by 1
-6x - 2y = 22 * 2
-12x + 10y = -26 * 1
This becomes
-6x * 2 - 2y* 2 = 22*2
-12x*1 + 10y *1 = -26 * 1
-12x - 4y = 44------------------- equation 3
-12x + 10y = -26 --------------- equation 4
To eliminate x, substract equation 4 from equation 3
-12x - (-12x) - 4y - (10y) = 44 - (-26)
-12x + 12x -4y -10y = 44 + 26
0 - 14y = 70
-14y = 70
Divide both sides by -14

To find x, substitute the value of y = -5 into equation 1
-6x - 2y = 22
-6x - 2(-5) = 22
-6x + 10 = 22
-6x = 22 - 10
-6x = 12
Divide both sides by -6
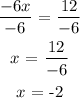
Hence, x = -2, and y = -5 : (-2, -5)