Question

Which is a step in creating the graph of a quadratic inequality? A) Choose a test point from the unshaded area to substitute back into the original quadratic inequality to confirm that a true statement results. B) Graph the parabola, using a dotted line for a strict inequality and a solid line for a non-strict inequality. C) Use the equality sign to determine where to shade. D) Leave the inequality as is in the statement.

Answer 1

The correct step in creating the graph of a quadratic inequality is:

C) Use the equality sign to determine where to shade.

When graphing a quadratic inequality, you first graph the corresponding quadratic equation (with an equality sign) to find the boundary of the solution set. After that, you use the equality sign to determine whether the boundary itself is included in the solution set or not. If it is included, you use a solid line; if it is not included, you use a dotted line. Finally, you shade the region that satisfies the inequality.

Certainly! Let's break down the process of graphing a quadratic inequality step by step:

1. Graph the Corresponding Quadratic Equation:

- Start by graphing the quadratic equation that corresponds to the inequality. For example, if you have the inequality
`\(y < ax^2 + bx + c\)`, graph the quadratic equation
`\(y = ax^2 + bx + c\)`.

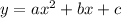- This graph represents the boundary or the "equal to" part of the solution.

2. Use a Solid or Dotted Line:

- If the inequality is of the form
`\(y \leq ax^2 + bx + c\) or \(y \geq ax^2 + bx + c\)`, then the boundary is included in the solution. Use a **solid line** to represent this.

- If the inequality is of the form
`\(y < ax^2 + bx + c\) or \(y > ax^2 + bx + c\)`, then the boundary is not included in the solution. Use a dotted line to represent this.

3. Determine the Shading:

- The next step is to determine where to shade. To do this, you use the equality sign
`(\(=\))` in the corresponding quadratic equation.

- If the equality sign is
`\(=\) or \(\leq\)` in the equation, shade the region below the graph for a downward-opening parabola or above the graph for an upward-opening parabola.

- If the equality sign is
`\(=\) or \(\geq\)`, shade the region above the graph for a downward-opening parabola or below the graph for an upward-opening parabola.

4. Test a Point (Optional):

- To confirm your shading, you can choose a test point from one of the shaded or unshaded regions and substitute it back into the original inequality. If the statement is true, you've correctly shaded the solution set.

So, in summary, creating the graph of a quadratic inequality involves graphing the corresponding quadratic equation, using a solid or dotted line based on the type of inequality, and then determining the shading by considering the equality sign in the equation.