Question

Given line j is parallel to line k, determine the value of x.

x = 18

x = 10

x = 28

x = 20

Answer 1

x = 10

Explanation:

Alternate exterior angles are a pair of angles that are formed on the outer side of two parallel lines but on opposite sides of a transversal. They are called alternate because they are on opposite sides of the transversal, and exterior because they are on the outside of the parallel lines.

Alternate exterior angles are always congruent.

In this case:

(x + 10)° and (4x - 20)° are alternate exterior angles.

So, they are equal to each other.

(x + 10)° = (4x - 20)°

Add 20 on both sides:

(x + 10 + 20)° = (4x - 20 + 20)°

(x + 30)° = (4x)°

Subtract x on both sides.

(x + 30 - x)° = (4x - x)°

30 = 3x

Divide both sides by 3.

`\sf (30)/(3)=(3x)/(3)`

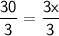
10 = x

x = 10

So, the value of x is 10.

Answer 2

x = 10

Step-by-step explanation:

Given line j is parallel to line k.

Then, the angles shown on the image are alternate exterior angles.

• So, we can write the following equation to find the value of x:

4x - 20 = x + 10

• Transfer variables to the same side of the equation.

4x - x = 10 + 20

• Add/subtract.

3x = 30

• Divide both sides by 3.

x = 10