Question

Write an equation for the line parallel to the given line that contains B. B(3, 8) ; y = - 4x + 7

Answer 1

You have to write an equation parallel to the line: y=-4x+7 that crosses the point (3,8)

One characteristic that two parallel lines share is that they have the same slope.

The slope for the known line corresponds to the coefficient multiplying the x-term and is m=-4

The line you have to find must have the same slope.

Using the point-slope form you can determine said line. The general structure is:

`y-y_1=m(x-x_1)`

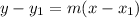
Where

m is the slope

x₁, y₁ are the coordinates of a point crossed by the line.

Using (3, 8) and m=-4

`y-8=-4(x-3)`

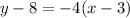
Now you have to solve it and write it in slope-intercept form. First step is to solve the term in parentheses by applying the distributive propperties of multiplication:

`\begin{gathered} y-8=-4x-3\cdot(-4) \\ y-8=-4x+12 \end{gathered}`

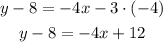
Next pass "-8" to the other side of the equal sign:

`\begin{gathered} y-8+8=-4x+12+8 \\ y=-4x+20 \end{gathered}`

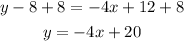
The equation for the line parallel to y=-4+7 is y=-4x+20