Question

Please show full solutions and all calculations that led to the final answer! Thank you so much!!

Answer 1

see explanation

Explanation:

a)

v(t) = 6t^2-25t-20
a(t) = 12t-25

explanation: take the derivative s(t) to get v(t), then take the derivative of v(t) to get a(t).

b) v(3)=6(3)^2-25(3)-20
velocity at 3 seconds = -41 m/s
a(3)=12(3)-25
acceleration at 3 seconds = 11 m/s^2

explanation: plugin 3 to both the velocity and acceleration functions

c) 6t^2-25t-20=0

x=(-sqrt(1105)+25))/12 or x=(sqrt(1105)+25))/12

set v(t) function equal to zero and factor through the means of quadratic formula

d) negative direction: v(t)<0

(sqrt(1105)+25)/12, infinity)

plugged in a number that was bigger than the largest x, and got out a negative number. therefore, anything larger than (sqrt(1105)+25)/12 is traveling left, or in the negative direction.

Answer 2

`\begin{aligned}\textsf{(a)}\quad v(t)&=6t^2-25t-20\\a(t)&=12t-25\end{aligned}`

`\begin{aligned}\textsf{(b)}\quad v(3)&=-41\;\sf m/s\\a(3)&=11\; \sf m/s^2\end{aligned}`

`\textsf{(c)}\quad 4.85\; \sf s\;(3\;s.f.)`

`\textsf{(d)}\quad 0 \leq t < 4.85`

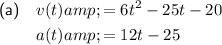
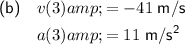
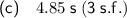
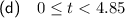
Explanation:

The displacement of a particle moving in a straight line is given by the equation:

`s(t)=2t^3-12.5t^2-20t-4, \quad t\geq 0`

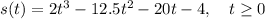
where:

• s(t) is the position in meters.
• t is the time in seconds.

The relationships between displacement, velocity and acceleration are:

`\boxed{\boxed{\begin{array}{c}\textbf{DISPLACEMENT (s)}\\\\\text{Differentiate} \downarrow\qquad\uparrow\text{Integrate}\\\\\textbf{VELOCITY (v)}\\\\\text{Differentiate}\downarrow\qquad\uparrow \text{Integrate}\\\\\textbf{ACCELERATION (a)}\end{array}}}`

`\hrulefill`

Part (a)

To find the equation for velocity v(t), we can differentiate the equation for displacement s(t):

`\begin{aligned}v(t)&=s'(t)\\v(t)&=3\cdot 2t^(3-1)-2\cdot 12.5t^(2-1)-20-0\\v(t)&=6t^2-25t-20\end{aligned}`

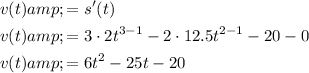
To find the equation for acceleration a(t), we can differentiate the equation for velocity v(t):

`\begin{aligned}a(t)&=v'(t)\\a(t)&=2\cdot 6t^(2-1)-25-0\\a(t)&=12t-25\end{aligned}`

`\hrulefill`

Part (b)

To determine the particle's velocity and acceleration at 3 seconds, simply substitute t = 3 into the equations found in part (a):

`\begin{aligned}v(3)&=6(3)^2-25(3)-20\\&=6(9)-25(3)-20\\&=54-75-20\\&=-41\; \sf m/s\end{aligned}`

`\begin{aligned}a(3)&=12(3)-25\\&=36-25\\&=11\; \sf m/s^2\end{aligned}`

`\hrulefill`

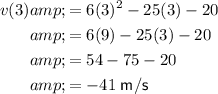
Part (c)

The particle will be at rest when its velocity is equal to zero. Therefore, to determine at what time(s) the particle will be at rest, set v(t) = 0 and solve for t using the quadratic formula.

`\boxed{\begin{array}{l}\underline{\sf Quadratic\;Formula}\\\\x=(-b \pm √(b^2-4ac))/(2a)\\\\\textsf{when} \;ax^2+bx+c=0 \\\end{array}}`

In the case of 6t² - 25t - 20 = 0:

• a = 6
• b = -25
• c = -20

Substitute these values into the quadratic formula and solve for t:

`t=(-(-25)\pm√((-25)^2-4(6)(-20)))/(2(6))`

`t=(25\pm√(1105))/(12)`

`t=4.85346168976...\; \sf s`

`t=-0.68679502309... \; \sf s`

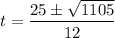
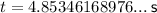
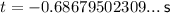
As t ≥ 0, the particle will be at rest at 4.85 s (3 s.f.) only.

`\hrulefill`

Part (d)

The particle is moving in the negative direction when the velocity v(t) is negative, so when v(t) < 0.

We already found the critical values when we found v(t) = 0. So, we need to test the values on either side of the critical numbers to determine when the particle is moving in the positive or negative direction.

`v(4.84)&=6(4.84)^2-25(4.84)-20=-0.4464 < 0`

`v(4.86)&=6(4.86)^2-25(4.86)-20=0.2176 > 0`

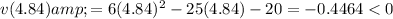
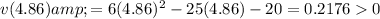
Therefore, as velocity is negative when 0 ≤ t < 4.85, the particle is moving in the negative direction in the interval 0 ≤ t < 4.85 (rounded to 3 s.f.).