Given:
The mass of the spheres is m = 4.982 g
The distance between the center of spheres is d = 3.173 cm
The acceleration is a = 258.312 m/s^2.
To find the magnitude of charge in micro Coulomb on each sphere.
Step-by-step explanation:
According to Newton's second law, the force will be
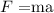
According to Coulomb's law, the force will be
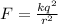
Here, k is the Coulomb's constant whose value is
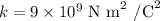
On equating the forces, the charge will be
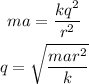
On substituting the values, the magnitude of charge will be
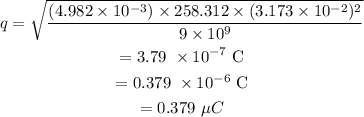
The magnitude of the charge of each sphere is 0.379 microCoulomb