Question

2. Calculate the distance MI for the length of the zipline cable. 3. Calculate the angle at which our zipliners will be descending toward the island . Safety regulations state that the angle at which a zipline cable meets the launching point cannot be smaller than 68 degrees . Please determine if we are in compliance with these regulations

Answer 1

right

`\begin{gathered} AI)\text{ 400 ft} \\ MI)412.31\text{ f} \\ \text{angle = 76} \end{gathered}`

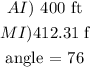
Step-by-step explanation

Step 1

AI?

we have a rigth triangle

then

let

`\begin{gathered} AB=side1 \\ AI=side\text{ 2} \\ IB=\text{ hypotenuse} \end{gathered}`

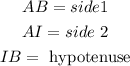
we can use the pythagorean Thoerem to find the missing vale

so

`\begin{gathered} (AB)^2+(AI)^2=(BI)^2 \\ \text{replace} \\ 300^2+(AI)^2=500^2 \\ so \\ (AI)^2=500^2-300^2 \\ AI=\sqrt[]{500^2-300^2}=\sqrt[]{160000}=400 \\ AI=400 \end{gathered}`

Step 2

MI?

let

`\begin{gathered} \text{angle}=x \\ \text{opposite side=100 m} \\ \text{adjacent side=400 m} \end{gathered}`

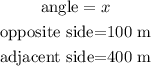
so, we need a function that relates those 3 values

`\tan \theta=\frac{opposite\text{ side}}{\text{adjacent side}}`

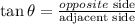
replace

`\begin{gathered} \tan \theta=\frac{opposite\text{ side}}{\text{adjacent side}} \\ \tan x=(400)/(100) \\ \tan x=4 \\ \text{hence} \\ x=\tan ^(-1)(4) \\ x=75.96 \\ \text{rounded} \\ x=76\text{ \degree} \end{gathered}`

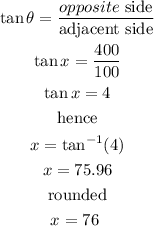
As 76 is greater than 68, the zipline cable compliance with these regulations.

Also, the hypotenuse (zipline ) is

`\begin{gathered} (MI)^2=(AI)^2+(AM)^2 \\ \text{replace} \\ (MI)^2=(400)^2+(100)^2 \\ (MI)^2=170000 \\ MI=\sqrt[]{17000} \\ MI=412.31\text{ ft} \end{gathered}`

I hope this helps you