Question

D. The number of people in the United States with mobile cellular phones was about 142

million in 2002 and about 255 million in 2007. If the growth in mobile cellular phones
was linear, what was the approximate rate of growth per year from 2002 to 2007?
What would the expected number of people to have phones in 2010? 2015? 2020?
Show this information on a graph (years versus the number of users).

Answer 1

Since it is linear, we can assume a function of the form:

`y(x)=mx+b`

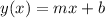
Where:

m = Slope = rate of growth

b = y-intercept

So:

`\begin{gathered} x=2002,y=142 \\ 142=2002m+b_{\text{ }}(1) \\ ----------- \\ x=2007,y=255 \\ 255=2007m+b_{\text{ }}(2) \end{gathered}`

Using elimination method:

`\begin{gathered} (2)-(1) \\ 255-142=2007m-2002m+b-b \\ 113=5m \\ m=(113)/(5)=22.6 \end{gathered}`

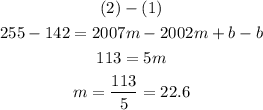
So:

Replace m into (1):

`\begin{gathered} 142=2002(22.6)+b \\ b=-45103.2 \end{gathered}`

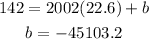
The linear equation which represents this model is:

`y=22.6x-45103.2`

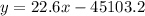
The approximate rate of growth per year from 2002 to 2007 is 22.6 million

the expected number of people to have phones in:

`\begin{gathered} x=2010 \\ y=22.6(2010)-45103.2 \\ y\approx323 \end{gathered}`
`\begin{gathered} x=2015 \\ y=22.6(2015)-45103.2 \\ y\approx436 \end{gathered}`
`\begin{gathered} x=2020 \\ y=22.6(2010)-45103.2 \\ y\approx549 \end{gathered}`

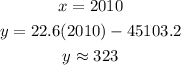
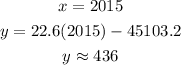
323 million of people will have phones in 2010

436 million of people will have phones in 2015

549 million of people will have phones in 2020