We could write the following equations according to the problem:
Hours equation:
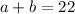
And, the payment equation: (cents)
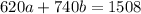
We could solve this system of equations using the elimination method:
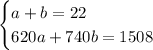
We're going to multiply the first equation by -620:
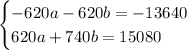
Now, we're going to sum both equations eliminating variable a, so we get a linear equation in terms of b:
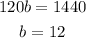
Now we know that he did 12 hours at job b.
As he worked 22 hours in total, then he worked 10 hours at job a.