Question

Given sec(x) = 3/2 and 3π/2 < x < 2π, find cos(x/2)

Answer 1

`\cos\left((x)/(2)\right)= -(√(30))/(6)`

Explanation:

To find cos(x/2) given the value of sec(x) and the constraint 3π/2 < x < 2π, we can use the properties of trigonometric functions and the cosine half-angle identity.

As sec(x) is the reciprocal of cos(x), and sec(x) = 3/2, then:

`\sec(x)=(3)/(2)`

`(1)/(\cos(x))=(3)/(2)`

`\cos(x)=(2)/(3)`

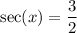
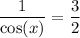
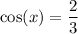
Next, we can find cos(x/2) by using the cosine half-angle identity:

`\boxed{\begin{array}{c}\underline{\textsf{Cosine Half Angle Identity}}\\\\\cos\left((x)/(2)\right)=\pm \sqrt{(1+\cos x)/(2)}\end{array}}`

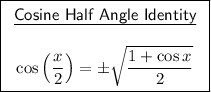
Substitute the found value of cos(x):

`\cos\left((x)/(2)\right)=\pm \sqrt{(1+(2)/(3))/(2)}`

`\cos\left((x)/(2)\right)=\pm \sqrt{((3)/(3)+(2)/(3))/(2)}`

`\cos\left((x)/(2)\right)=\pm \sqrt{((5)/(3))/(2)}`

`\cos\left((x)/(2)\right)=\pm \sqrt{(5)/(6)}`

`\cos\left((x)/(2)\right)=\pm (√(5))/(√(6))`

`\cos\left((x)/(2)\right)=\pm (√(5)\cdot √(6))/(√(6)\cdot √(6))`

`\cos\left((x)/(2)\right)=\pm (√(30))/(6)`

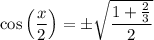
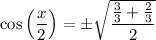
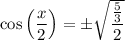
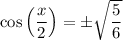
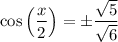
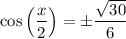
The given constraint for x is 3π/2 < x < 2π.

Therefore, the constraint for x/2 is 3π/4 < x/2 < π, which is in quadrant II. Cosine is negative in quadrant II, so we can take the negative square root:

`\cos\left((x)/(2)\right)= -(√(30))/(6)`

Therefore, cos(x/2) = -√(30)/6 for the given values of sec(x) and the interval 3π/2 < x < 2π.