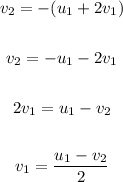Question

Object 1 has a mass (M1) and a velocity (V1). Object 2 has a mass half the size of object 1 and a velocity that is 3 times the speed, but in the opposite direction. They collide in a linear elastic collision. Find the final velocity of both objects in terms of M1 and V1. (reduce the final answer to one term, reduced as much as possible with no fractions or decimals in major divisions)

Answer 1

Answer:
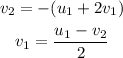
`\begin{gathered} v_2=-(u_1+2v_1) \\ v_1=(u_1-v_2)/(2) \end{gathered}`Step-by-step explanation:

Mass of object 1 = m₁

Velocity of object 1, = u₁

The mass of object 2 is half that of object 1

m₂ = m₁/2

The velocity of object 2 is three times the speed of object 1 but in the opposite direction

u₂ = -3u₁

The final velocity of both object is represented by v

Applying the principle of momentum conservation

`\begin{gathered} m_1u_1+m_2u_2=m_1v_1+m_2v_2 \\ \\ m_1u_1+(1)/(2)m_1(-3u_1)=m_1v_1+(1)/(2)m_1v_2 \\ \\ m_1u_1-(3(m_1u_1))/(2)=(2m_1v_1+m_1v_2)/(2) \\ \\ (2m_1u_1-3m_1u_1)/(2)=(2m_1v_1+m_1v_2)/(2) \\ \\ -m_1u_1=2m_1v_1+m_1v_2 \\ \\ m_1v_2=-m_1u_1-2m_1v_1 \\ \\ v_2=(-m_1(u_1+2v_1))/(m_1) \\ \\ v_2=-(u_1+2v_1) \\ \\ \end{gathered}`

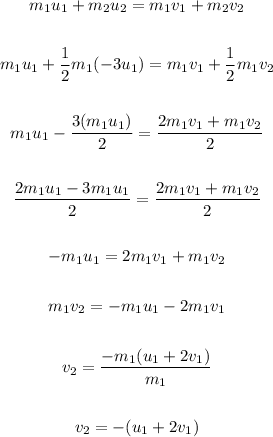
From the last equation, make v₁ the subject of the formula instead

`\begin{gathered} v_2=-(u_1+2v_1) \\ \\ v_2=-u_1-2v_1 \\ \\ 2v_1=u_1-v_2 \\ \\ v_1=(u_1-v_2)/(2) \\ \\ \end{gathered}`