Question

Solve by factoring.
5x^2 - 45x + 100

Please give step-by-step explanation :)

Answer 1

x = 4 and x = 5

Explanation:

`\sf 5x^2 - 45x + 100 = 0`

We notice that all the terms in the quadratic equation are divisible by 5, so we can factor out a 5:

`\sf 5(x^2 - 9x + 20) = 0`

Now we need to factor the expression x² - 9x + 20.

We can use the sum-product pattern, which states that x² + bx + c can be factored as (x + a)(x + b) if a + b = b and ab = c.

In this case, we want to find values for a and b that satisfy the following conditions:

• a + b = -9
• ab = 20

We can start by trying to guess which factors of 20 add up to -9.

The factors -5 and -4 satisfy both conditions, so we can factor the expression as follows:

`\sf x^2 - 9x + 20 = (x - 5)(x - 4)`

Now we can substitute this factored expression back into the original equation:

`\sf 5(x - 5)(x - 4) = 0`

Since the entire equation is equal to zero, one or both of the factors must be equal to zero.

So,

either

`\sf (x-5)= 0`

`\sf x = 5`

or

`\sf (x-4)= 0`

`\sf x = 4`

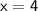
Therefore, the solutions to the equation are x = 4 and x = 5.

Answer 2

x = 4 and x = 5

=================

Given quadratic equation:

• 5x² - 45x + 100 = 0

First, factor out 5:

• 5(x² - 9x + 20) = 0

Next, cancel 5:

• x² - 9x + 20 = 0

Now, find two numbers whose product is 20 and sum is 9. By testing we can find the two numbers are 4 and 5.

Rearrange the equation:

• x² - 5x - 4x + 20 = 0
• x(x - 5) - 4(x - 5) = 0

Factor out the common binomial (x - 5):

• (x - 5)(x - 4)

Set each factor equal to zero and solve for x:

• x - 4 = 0 ⇒ x = 4
• x - 5 = 0 ⇒ x = 5

Therefore, the solutions are x = 4 and x = 5.