Question

In the diagram,ABCD is a rectangular wall that casts a shadow CDEF, on the ground. The wall has a height of 4 feet. The shadow is a parallelogram that has a height, FG, that is twice the height of the wall. If the area of the wall is 29.2 square feet, find the area of the shadow.

Answer 1

We know that the height of the rectangular shape is BC=AD= 4 feet and the the area is A=29.2 ft^2. Since the area of our rectangle is given by

`A=(DC)*(BC)`

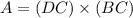
we get

`29.2=DC*4`

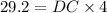
By moving the number 4 to the left hand side, we have

`\begin{gathered} (29.2)/(4)=DC \\ \text{then} \\ DC=7.3 \end{gathered}`

which also is the lenght of one side of our parallelogram.

Now, the area of our parallelogram is given by

`A_P=\text{base}* height`

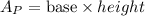
where the base is given by segment DC=7.3 ft and the height FG=2 BC. Then, we get

`\begin{gathered} A_P=DC* FG \\ A_P=DC*2BC \end{gathered}`

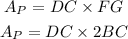
by substituting our previous result and BC=4 ft, we obtain

`\begin{gathered} A_P=7.3*2(4) \\ A_P=7.3*8 \\ A_P=58.4ft^2 \end{gathered}`

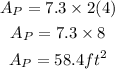
Then, the answer is 58.4 ft^2