Question

What is the area of a triangle whose vertices are R(3, 4), S(8, 4) and T(8, 10)?

Answer 1

Answer:15

Step-by-step explanation: i took the test

Answer 2

15 square units

Explanation:

Given:

Vertices: R(3, 4), S(8, 4) and T(8, 10)

To find the area of a triangle we can use the distance formula, we first need to find the lengths of the three sides of the triangle. and finding out area using Heron's formula.

Using the distance formula, we can find the following:

`\textsf{Distance }=√((x_2-x_1)^2 + (y_2-y_1)^2)`

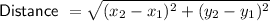
Where,

`(x_1,y_1)` and
`(x_2,y_2)` are coordinate.

In this case:

Using this:

`\sf RS = √((3 - 8)^2 + (4 - 4)^2) \\\\ = √((-5)^2+(0)^2) \\\\ = √(25) \\\\ = 5`

`\sf ST = √((8 - 8)^2 + (4 - 10)^2) \\\\ = √((0)^2 + (-6)^2) \\\\ = √(36)\\\\ = 6`

`\sf TR = √((3 - 8)^2 + (4 - 10)^2) \\\\ =√((-5)^2 + (-6)^2) \\\\ = √(25+36)\\\\ = √(61) \\\\ = 7.8`

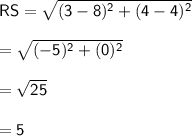
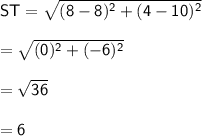
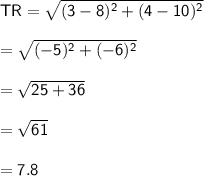
Now that we have the lengths of the three sides, we can use Heron's formula to find the area of the triangle:

`\boxed{\boxed{\sf Area = √(s(s - a)(s - b)(s - c))}}`

where s is the semi-perimeter of the triangle, which is equal to half the sum of the lengths of the three sides:

`\sf s = (5 + 6 + 7.8 )/(2) \\\\ = (18.8)/(2)\\\\ = 9.4`

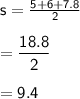
Substituting the values of s, a, b, and c into Heron's formula and simplifying it.

`\sf Area = √(9.4 (9.4 - 5)(9.4 - 6)(9.4-7.8)) \\\\ = √( 9.4 (4.4 )(3.4 )(1.6) ) \\\\ = √( 224.9984) \\\\ = 14.999946666571 \\\\ = 15 \textsf{(in nearest tenth )}`

Therefore, the area of the triangle is 15 square units.