Question

Conner left his house and rode his bike into town at 6mph. Along the way he got a flat tire so he had to turn around and walk his bike to his house traveling 3 mph. If the trip down and back took 15 hours, how far did he get before his tire went flat?Conner went ___ miles before his tire went flat.

Answer 1

The main point in this question, that the distance of the first part = the distance of the second part

`d_1=d_2`

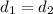
Since the speed of the first part is 6 mph

Let the time of it be t1

Since distance = speed x time, then

`\begin{gathered} d_1=v_{1_{}}* t_1_{} \\ d_1=6* t_1 \\ d_1=6t_1 \end{gathered}`

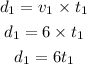
Since the speed of the second part is 3 mph

Let the time of it be t2, then

`\begin{gathered} d_2=3* t_2 \\ d_2=3t_2 \end{gathered}`

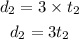
Equate d1 and d2 to find t2 in terms of t1

`3t_2=6t_1`

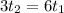
Divide both sides by 3

`\begin{gathered} (3t_2)/(3)=(6t_1)/(3) \\ t_2=2t_1\rightarrow(1) \end{gathered}`

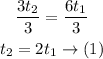
Since the total time of the two parts is 15 hours, then

`t_1+t_2=15\rightarrow(2)`

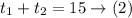
Substitute (1) in (2)

`\begin{gathered} t_1+2t_1=15 \\ 3t_1=15 \end{gathered}`

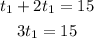
Divide both sides by 3

`\begin{gathered} (3t_1)/(3)=(15)/(3) \\ t_1=5 \end{gathered}`

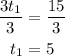
Now, let us find d1

`\begin{gathered} d_1=6*5 \\ d_1=30 \end{gathered}`

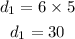
Conner went 30 miles before his tire went flat