We have a closed container, so the number of moles remains constant.
Now, the total pressure is equal to the sum of the partial pressures. And the partial pressure of a gas will depend on its molar fraction, that is, the moles of the gas over the total moles. So the partial pressure is defined as:
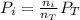
Where,
Pi is the partial pressure of the gas
ni, are the moles of the corresponding gas
nT, are the total moles
Pt is the total pressure.
1. Partial pressures of O2 and CO2
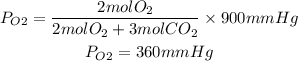
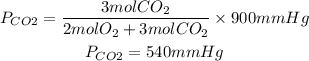
Answer: PO2=360mmHg
PCO2=540mmHg
2. Now, the density will depend of the number of moles and the volume. We can calculate the volume of the gases with the ideal gas equation that says:

For each gas we will have:
O2
PO2=340mmHg=0.45atm
T=37°C=310.15K
R is a constant = 0.08206 (atm.L)/(mol.K)
nO2=2mol
massO2=2mol x MolarMass = 2 mol x 31.998g/mol=63.996g
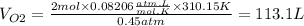
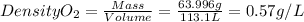
CO2
PCO2=540mmHg=0.71atm
T=37°C=310.15K
R is a constant = 0.08206 (atm.L)/(mol.K)
nCO2=3mol
massCO2=3mol x MolarMass = 3 mol x 44.01g/mol=132.03g
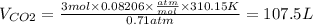

Answer:
Density O2=0.57g/L
Density CO2 = 1.23g/L
3. In the second situation, what will happen is that the partial pressure of the gases will decrease, since due to the pressure exerted by the piston, part of the moles of gas will dissolve in the water. So in the gas phase we will have fewer moles of gas.