Question

Calculate the difference quotient and use your results to find the slope of the tangent line

Answer 1

Approximate Slope of a Function

We are given the function:

`H(x)=8\ln x+3`

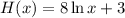
We will find the approximate value of the slope at (e,11).

It's required to use 3 possible values of the approximation differential h.

Let's use h=0.1 and evaluate the function at x = e + 0.1 = 2.8182818

Compute:

`H(e+0.1)=8\ln 2.8182818+3=11.2890193`

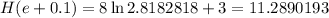
Compute the difference quotient:

`H^(\prime)=(11.2890193-11)/(0.1)=2.890193`

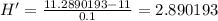
Now we use h=0.01:

`H(e+0.01)=8\ln 2.728281828+3=11.02937635`

The difference quotient is:

`H^(\prime)=(11.02937635-11)/(0.01)=2.9376353`

Finally, use h=0.001:

`H(e+0.001)=8\ln 2.719281828+3=11.00294249`
`H^(\prime)=(11.00294249-11)/(0.001)=2.9424943`

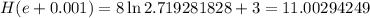
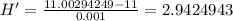
The last result is the most accurate, thus the slope of the tangent line is 2.94