Answer:
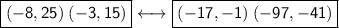
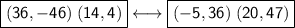
Explanation:
The slope of a line perpendicular to the original line is the negative reciprocal of the original slope. Therefore, to calculate the perpendicular slope between two points, find the slope of the original line that passes through these points using the slope formula, then take its negative reciprocal.


Points (-8, 25) and (-3, 15)
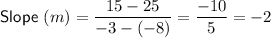
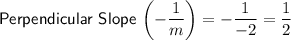
Points (-17, -1) and (-97, -41)
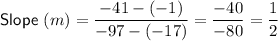
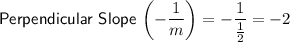
Therefore, the slope of the line that passes through points (-8, 25) and (-3, 15) is perpendicular to the slope of the line that passes through points (-17, -1) and (-97, -41), and vice versa.

Points (36, -46) and (14, 4)
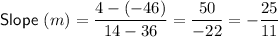
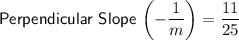
Points (-5, 36) and (20, 47)
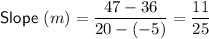
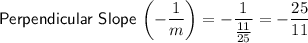
Therefore, the slope of the line that passes through points (36, -46) and (14, 4) is perpendicular to the slope of the line that passes through points (-5, 36) and (20, 47), and vice versa.