Question

Find the rate of change of (1/4, 1/2) and (1/6, 1/3)

Answer 1

Rate of change = 2

Explanation:

The rate of change (aka the slope) is:

the change in y / the change in x

Since the rate of change is synonymous with the slope, we can find it using the slope formula, which is given by:

`m=((y_(2)-y_(1)) )/((x_(2)-x_(1)) )`, where:

• m is the rate of change,
• (x1, y1) is one point,
• and (x2, y2) is another point.

Thus, we can find the rate of change by substituting (1/4, 1/2) for (x1, y1) and (1/6, 1/3) for (x2, y2) in the slope formula:

`m=((1/3-1/2))/((1/6-1/4))\\ \\m=((-1/6))/((-2/24))\\ \\m=((-1/6))/((-1/12))\\ \\m=(-1)/(6)*-12\\ \\m=12/6\\\\m=2`

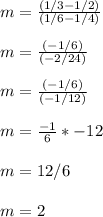
Therefore, the rate of change of (1/4, 1/2) and (1/6, 1/3) is 2.

Answer 2

24 over 23 because it simplifies to 2/3