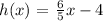Two lines are parallel if they have the same slope. In order to better visualize the slope of the line we will express it in the slope-intercept form, which is done below:
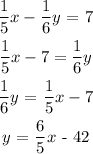
We now know that the slope of the line is 6/5, because in this form the slope is always the number that is multiplying the "x" variable. So we need to find a line of the type:
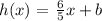
Therefore the only needed variable is "b", which we can find by applying the known point (-5, -10).
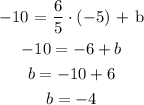
The expression of the line is then: