In order to solve the system of equations, let's equate both values of y and solve for x using the quadratic formula:
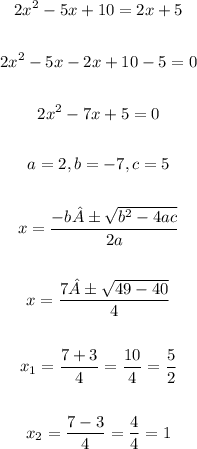
Now, let's calculate the values of y for each value of x:
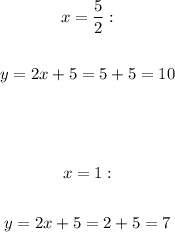
Therefore the solutions are (1, 7) and (5/2, 10).
Correct option: second one.