Question

Need a step by step answer as soon as possible (30 points)​

Answer 1

`\cfrac{y^4* y^n}{y^2}~~ = ~~y^(-3)\implies \cfrac{y^(4+n)}{y^2}~~ = ~~y^(-3)\implies y^(4+n)* y^(-2)=y^(-3) \\\\\\ y^(4+n-2)=y^(-3)\implies 4+n-2=-3\implies 2+n=-3\implies \boxed{n=-5}`

Answer 2

n = -5

Explanation:

You want the value of n in the equation ...

`(y^4* y^n)/(y^2)=y^(-3)`

Exponents

The relevant rules of exponents are ...

(a^b)(a^c) = a^(b+c)

(a^b)/(a^c) = a^(b-c)

Application

Applying those rules to the given equation, we have ...

`(y^4* y^n)/(y^2)=y^(4+n-2)=y^(2+n)=y^(-3)`

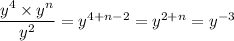
Equating exponents gives ...

2 +n = -3

n = -5 . . . . . . . . . subtract 2

The value of n is -5.

__

Additional comment

It can be helpful to think of an exponent as indicating repeated multiplication. The usual rules for simplifying products and quotients apply.

That is, y⁴ = y·y·y·y. So, y⁴/y² is ...

`(y^4)/(y^2)=(y\cdot y\cdot y\cdot y)/(y\cdot y)=y\cdot y = y^2`

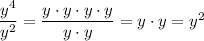
<95141404393>