1 Answer

Michael Eliot · Answer 1 · 2023-10-29T03:14:05+0000

Given: Two points

$\begin{gathered} Point1:(10,11) \\ Point2:(10,7) \end{gathered}$
$\begin{gathered} Point1:(10,11) \\ Point2:(10,7) \end{gathered}$

To Determine: The equation of the line in standard form that passes through the given points

Solution

The equation of a line passing through two different points is given as

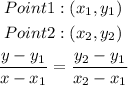
$\begin{gathered} Point1:(x_1,y_1) \\ Point2:(x_2,y_2) \\ (y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1) \end{gathered}$

Substitte the given coordinates of the points given into the formula

$\begin{gathered} (y-11)/(x-10)=(7-11)/(10-10) \\ (y-11)/(x-10)=(-4)/(0) \\ cross-multiply \\ Since\text{ the slope is undefine} \\ The\text{ equation of the line is } \\ x=10 \end{gathered}$

The standard form of a line is given as

But since the x-coordinates of the points are equal, then the formula for slope is not applicable (the denominator equals 0).

In this case, we say that the slope is undefined (the line is vertical).

This means that the equation of the line doesn't contain y.

Thus, the equation of the line is x=10.

Answer: the slope is undefined.

The equation of the line is x = 10.

0 Comments

Your comment on this question:

Your answer

1 Answer

0 Comments

Your comment on this answer:

Other Questions