Question

The first and last terms of an AP are 21 and - 47 respectively. If the sum of the series is given as - 234 calculate the number of terms in the AP

Answer 1

Number of terms = 18

Step-by-step explanation:

For an arithmetic progression, the sum of the series given first and last terms and the number of terms is given is given by the formula

S = n/2 (first-term + last-term) or rewritten as

S = n · (first-term + last-term)/2

Here we are given

S = -234

first-term = 21

last-term = -47

Substituting for knows in the S equation we can solve for n, the number of terms

`-234 = (n)/(2) (21 + (-47))\\\\-234 = (n)/(2) ( 21 - 47)\\\\-234 = (n)/(2) (-26)`

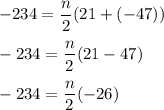
Switch sides:

`(n)/(2) (-26) = -234`

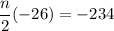
Dividing both sides by -26 :

`(n)/(2) = -234/-26`

`(n)/(2) = 9`

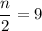
Multiply by 2 both sides

`(n)/(2) * 2 = 9 * 2\\\\n = 18`

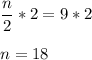
So total number of terms = 18

Answer 2

The number of terms in the arithmetic progression is 18.

Step-by-step explanation:

To find the number of terms in the arithmetic progression (AP), we need to use the formula for the sum of an AP. The formula is:

S = (n/2)(a + l), where S is the sum, n is the number of terms, a is the first term, and l is the last term.

Given that the first term (a) is 21, the last term (l) is -47, and the sum (S) is -234, we can plug in these values and solve for n:

-234 = (n/2)(21 + (-47))
-234 = (n/2)(-26)
-234 = -13n
n = -234/(-13)
n = 18