Question

Write an equation of the line passing through (-1,5) and (4,6). G The equation of the line in standard form is​

Answer 1

x - 5y = -26

Explanation:

To find the equation of the line passing through the points (-1, 5) and (4, 6), we can use the point-slope form of a linear equation:

`\sf y - y_1 = m(x - x_1)`

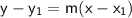
where (x₁, y₁) is one of the points on the line, and "m" is the slope of the line.

First, calculate the slope "m" using the two given points (-1, 5) and (4, 6):

`\sf m = (y_2 - y_1)/(x_2 - x_1) \\\\ = (6 - 5)/(4 - (-1))\\\\ = (1)/(5)`

Now that we have the slope, we can use either of the two points to write the equation. Let's use the point (-1, 5):

`\sf y - 5 = (1)/(5)(x - (-1))`

Simplify the equation:

`\sf y - 5 = (1)/(5)(x + 1)`

To eliminate fractions, we can multiply both sides of the equation by 5:

5(y - 5) = 1(x + 1)

Now, distribute on both sides:

5y - 25 = x + 1

The standard form of a linear equation is:

Ax + By = C

where A, B, and C are constants.

To write the equation in standard form, move all terms to one side and set it equal to zero:

x - 5y = -26

So, the equation of the line passing through the points (-1, 5) and (4, 6) in standard form is:

x - 5y = -26