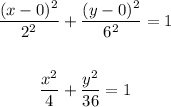As the given vertices are at a distance of 12 units:
As the major axis is vertical you have the next generall equation:
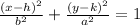
To find the center (h,k) of the ellipse use the coordinates of that vertices as follow:
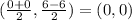
Now use the distance between those vertices to find a:
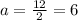
b is the distance of minor axis divided into 2:
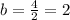
Then, you get the next equation for the given ellipse: