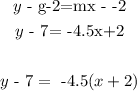Question

Can you find the correct answers to all parts of question 1 and 2. Could you also tell me why I got my answers wrong originally?

Answer 1

1.

Part a) G(x) is still a function because it's the inverse function of f(x).

part b)

f(g(4)).

FIrst step for this is to find g(4) which is:

`\begin{gathered} g(4)=f^{\text{ -1}}(4) \\ \\ g(4)=f^{\text{ -1}}(4)=g(4)=3 \end{gathered}`

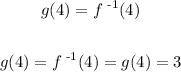
Part c)

Now, to find the equation of the tangent line we have to find the slope, which is the derivative, because the derivative is the slope of the tangent line at a given x-value

But they ask for the g function, in this case:

`\begin{gathered} f^{\text{ -1}}(\text{ -2\rparen} \\ then,\text{ g\lparen-2\rparen=7} \end{gathered}`

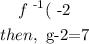
So, the derivative in f(x)= 7 is -4.5

So, the equation is:

`\begin{gathered} y\text{ - g\lparen-2\rparen=m\lparen x - \lparen-2\rparen} \\ y\text{ - 7= -4.5\lparen x+2\rparen} \\ \\ y\text{ - }7=\text{ -}4.5(x+2) \end{gathered}`