Question

Solve the system graphically and check the solution. 2x+y=4. Y-2x=6

Answer 1

`\begin{gathered} x\text{ = -0.5} \\ y\text{ = 5} \end{gathered}`

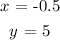
Step-by-step explanation:

Here, we want to solve the system of linear equations graphically, then we proceed to check for the solution

To do this, we have to plot the graph of the two equations on the same plot, the point at which these lines intersect would be the solution to the system of linear equations

We have the plot shown as follows:

From what we have on the plot, the solution to the system is x = -0.5 and y =5 . The reasonn for this is that it is at this point that both lines intersect

Now, let us check the solution:

We can check the solution by substituting -0.5 for x and 5 for y in both equations

For the first one:

`\begin{gathered} 2(-0.5)\text{ + 5 = 4} \\ -1\text{ + 5 = 4} \\ 4\text{ = 4} \end{gathered}`

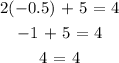
We can see that th solution works for the first equation

For the second one, we proceed with the same substitution process

We have this as:

`\begin{gathered} 5-2(-0.5)\text{ = 6} \\ 5\text{ + 1 = 6} \\ 6\text{ = 6} \end{gathered}`

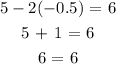
We can see the solution works for the second equation too