Given:
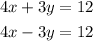
Required:
To solve the system of equation using graph and to state whether the system is dependent, independent, or inconsistent.
Step-by-step explanation:
Consider the equation
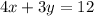
When x=0,
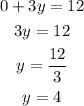
When x=3,
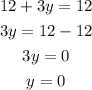
Now consider the equation
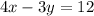
When x=0,
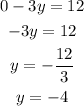
When x= 3,
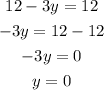
The graph of the given system of equation is,
The blue graph is graph of 4x+3y=12 and the black graph is graph of
4x-3y=12.
The two line crosses at the point (3,0).
Therefore the solution is
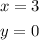
Here the solution is one.
Therefore the consistent system has exactly one solution, it is independent .
Final Answer:
The solution of the given system of equation is
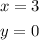
The consistent system has exactly one solution, it is independent .