Question

The denominator of a fraction is three more than the numerator

Answer 1

Let it be x the numerator. Then we have:

• x + 3: Denominator.

,

• x + 9: Numerator increased by nine.

,

• (x + 3) + 9: Denominator increased by nine.

Since the simplified result of the fraction is 13/14, we can write and solve for x the following equation.

`\begin{gathered} (x+9)/((x+3)+9)=(13)/(14) \\ (x+9)/(x+3+9)=(13)/(14) \\ (x+9)/(x+12)=(13)/(14) \\ \text{ Apply cross product} \\ (x+9)\cdot14=13\cdot(x+12) \\ \text{ Apply distributive property} \\ 14\cdot x+9\cdot14=13\cdot x+13\cdot12 \\ 14x+126=13x+156 \\ \text{ Subtract 126 from both sides } \\ 14x=13x+156-126 \\ 14x=13x+30 \\ \text{ Subtract 13x from both sides} \\ 14x-13x=13x+30-13x \\ x=30 \end{gathered}`

Now, we replace the value of x into the left expression from the equation we just solved.

`\begin{gathered} \text{ Original fraction }=(x+9)/((x+3)+9) \\ \text{ Original fraction }=(30+9)/(30+3+9) \\ \text{ Original fraction }=(39)/(42) \end{gathered}`

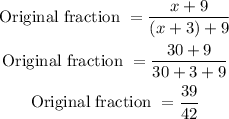
Therefore, the original fraction is 39/42.