Question

Parabola in the form x^2=4pyIdentify Vertex, value of P, focus, and focal diameter.Identify endpoints of latus rectumWrite equations for the directrix and axis of symmetry X^2= -12y

Answer 1

(a)

• The vertex of the parabola, (h,k)=(0,0)

,

• The value of p = -3

• The focus is at (0,-3).

,

• The focal diameter is 12

(b)The endpoints of latus rectum are (-1/12, -1/6) and (-1/12, 1/6).

(c)See Graph below

(d)

• I. The equation for the directrix is y=3.

,

• II. The axis of symmetry is at x=0.

Explanation:

Given the equation of the parabola:

`x^2=-12y`

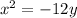
For an up-facing parabola with vertex at (h, k) and a focal length Ipl, the standard equation is:

`(x-h)^2=4p(y-k)`

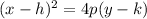
Rewrite the equation in the given format:

`\begin{gathered} (x-0)^2=4(-3)(y-0) \\ \implies(h,k)=(0,0) \\ \implies p=-3 \end{gathered}`

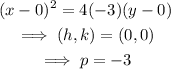
• The vertex of the parabola, (h,k)=(0,0)

,

• The value of p = -3

The focus is calculated using the formula:

`\begin{gathered} (h,k+p) \\ \implies Focus=(0,0-3)=(0-3) \end{gathered}`

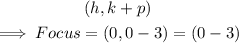
• The focus is at (0,-3).

Focal Diameter

Comparing the given equation with x²=4py, we have:

The focal diameter is 12

Part B (The endpoints of the latus rectum).

First, rewrite the equation in the standard form:

`\begin{gathered} y=-(1)/(12)x^2 \\ \implies a=-(1)/(12) \end{gathered}`

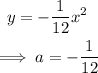
The endpoints are:

`\begin{gathered} (a,2a)=(-(1)/(12),-(1)/(6)) \\ (a,-2a)=(-(1)/(12),(1)/(6)) \end{gathered}`

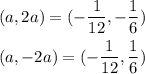
The endpoints of latus rectum are (-1/12, -1/6) and (-1/12, 1/6).

Part C

The graph of the parabola is given below:

Part D

I. The equation for the directrix is of the form y=k-p.

`\begin{gathered} y=0-(-3) \\ y=3 \end{gathered}`

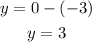
The equation for the directrix is y=3.

II. The axis of symmetry is the x-value at the vertex.

The axis of symmetry is at x=0.