Given:
(1985,46000)
(1997,38080)
(a)
General linear equation is:
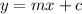
here y represent the population and x represent time so equation is:

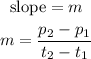
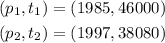
slope is:
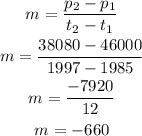
So equation is:

Point (1985,46000)

So equation is:
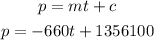
(b)
population in 2000.
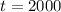
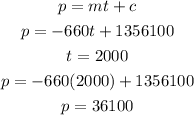
so population in 2000 is 36100.